Self-Organising Maps
Self-Organising Maps (SOMs) are an unsupervised data visualisation technique that can be used to visualise high-dimensional data sets in lower (typically 2) dimensional representations. In this post, we examine the use of R to create a SOM for customer segmentation. The figures shown here used use the 2011 Irish Census information for the greater Dublin area as an example data set. This work is based on a talk given to the Dublin R Users group in January 2014.
Note: This post has been updated for changes in the Kohonen API and R 3.2 in 2017.
If you are keen to get down to business:
The slides from a talk on this subject that I gave to the Dublin R Users group in January 2014 are available here (code is in the slides is *slightly* out of date now)
The updated code and data for the SOM Dublin Census data is available in this GitHub repository.
The code for the Dublin Census data example is available for download from here. (zip file containing code and data – filesize 25MB)
SOMs were first described by Teuvo Kohonen in Finland in 1982, and Kohonen’s work in this space has made him the most cited Finnish scientist in the world. Typically, visualisations of SOMs are colourful 2D diagrams of ordered hexagonal nodes.
The SOM Grid
SOM visualisation are made up of multiple “nodes”. Each node vector has:
- A fixed position on the SOM grid
- A weight vector of the same dimension as the input space. (e.g. if your input data represented people, it may have variables “age”, “sex”, “height” and “weight”, each node on the grid will also have values for these variables)
- Associated samples from the input data. Each sample in the input space is “mapped” or “linked” to a node on the map grid. One node can represent several input samples.
The key feature to SOMs is that the topological features of the original input data are preserved on the map. What this means is that similar input samples (where similarity is defined in terms of the input variables (age, sex, height, weight)) are placed close together on the SOM grid. For example, all 55 year old females that are appoximately 1.6m in height will be mapped to nodes in the same area of the grid. Taller and smaller people will be mapped elsewhere, taking all variables into account. Tall heavy males will be closer on the map to tall heavy females than small light males as they are more “similar”.
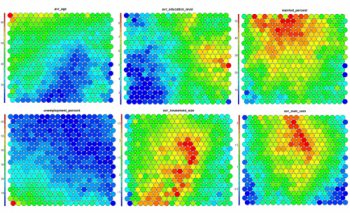
SOM Heatmaps
Typical SOM visualisations are of “heatmaps”. A heatmap shows the distribution of a variable across the SOM. If we imagine our SOM as a room full of people that we are looking down upon, and we were to get each person in the room to hold up a coloured card that represents their age – the result would be a SOM heatmap. People of similar ages would, ideally, be aggregated in the same area. The same can be repeated for age, weight, etc. Visualisation of different heatmaps allows one to explore the relationship between the input variables.
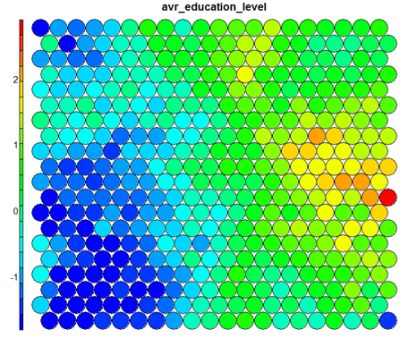
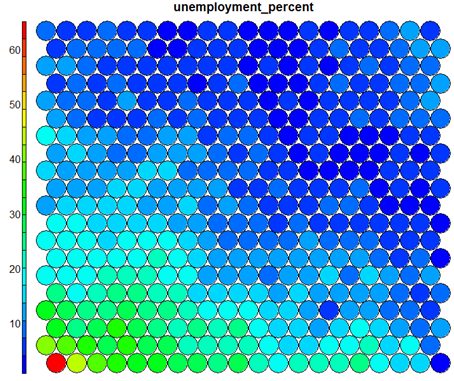
The figure below demonstrates the relationship between average education level and unemployment percentage using two heatmaps. The SOM for these diagrams was generated using areas around Ireland as samples.
SOM Algorithm
The algorithm to produce a SOM from a sample data set can be summarised as follows:
- Select the size and type of the map. The shape can be hexagonal or square, depending on the shape of the nodes your require. Typically, hexagonal grids are preferred since each node then has 6 immediate neighbours.
- Initialise all node weight vectors randomly.
- Choose a random data point from training data and present it to the SOM.
- Find the “Best Matching Unit” (BMU) in the map – the most similar node. Similarity is calculated using the Euclidean distance formula.
- Determine the nodes within the “neighbourhood” of the BMU.
– The size of the neighbourhood decreases with each iteration. - Adjust weights of nodes in the BMU neighbourhood towards the chosen datapoint.
– The learning rate decreases with each iteration.
– The magnitude of the adjustment is proportional to the proximity of the node to the BMU. - Repeat Steps 2-5 for N iterations / convergence.
Sample equations for each of the parameters described here are given on Slideshare.
SOMs in R
Training
The “kohonen” package is a well-documented package in R that facilitates the creation and visualisation of SOMs. To start, you will only require knowledge of a small number of key functions, the general process in R is as follows (see the presentation slides for further details):
# Creating Self-organising maps in R # Load the kohonen package require(kohonen) # Create a training data set (rows are samples, columns are variables # Here I am selecting a subset of my variables available in "data" data_train <- data[, c(2,4,5,8)] # Change the data frame with training data to a matrix # Also center and scale all variables to give them equal importance during # the SOM training process. data_train_matrix <- as.matrix(scale(data_train)) # Create the SOM Grid - you generally have to specify the size of the # training grid prior to training the SOM. Hexagonal and Circular # topologies are possible som_grid <- somgrid(xdim = 20, ydim=20, topo="hexagonal") # Finally, train the SOM, options for the number of iterations, # the learning rates, and the neighbourhood are available som_model <- som(data_train_matrix, grid=som_grid, rlen=500, alpha=c(0.05,0.01), keep.data = TRUE )
Visualisation
The kohonen.plot function is used to visualise the quality of your generated SOM and to explore the relationships between the variables in your data set. There are a number different plot types available. Understanding the use of each is key to exploring your SOM and discovering relationships in your data.
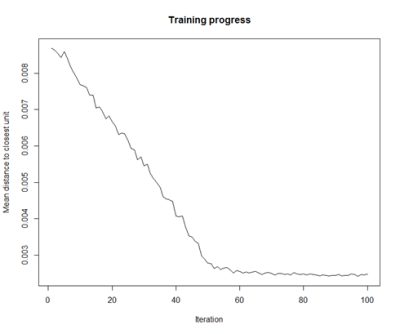
- Training Progress:
As the SOM training iterations progress, the distance from each node’s weights to the samples represented by that node is reduced. Ideally, this distance should reach a minimum plateau. This plot option shows the progress over time. If the curve is continually decreasing, more iterations are required.#Training progress for SOM plot(som_model, type="changes")
- Node Counts
The Kohonen packages allows us to visualise the count of how many samples are mapped to each node on the map. This metric can be used as a measure of map quality – ideally the sample distribution is relatively uniform. Large values in some map areas suggests that a larger map would be benificial. Empty nodes indicate that your map size is too big for the number of samples. Aim for at least 5-10 samples per node when choosing map size.#Node count plot plot(som_model, type="count", main="Node Counts")
- Neighbour Distance
Often referred to as the “U-Matrix”, this visualisation is of the distance between each node and its neighbours. Typically viewed with a grayscale palette, areas of low neighbour distance indicate groups of nodes that are similar. Areas with large distances indicate the nodes are much more dissimilar – and indicate natural boundaries between node clusters. The U-Matrix can be used to identify clusters within the SOM map.# U-matrix visualisation plot(som_model, type="dist.neighbours", main = "SOM neighbour distances")
- Codes / Weight vectors
Thenode weight vectors, or “codes”, are made up of normalised values of the original variables used to generate the SOM. Each node’s weight vector is representative / similar of the samples mapped to that node. By visualising the weight vectors across the map, we can see patterns in the distribution of samples and variables. The default visualisation of the weight vectors is a “fan diagram”, where individual fan representations of the magnitude of each variable in the weight vector is shown for each node. Other represenations are available, see the kohonen plot documentation for details.# Weight Vector View plot(som_model, type="codes")
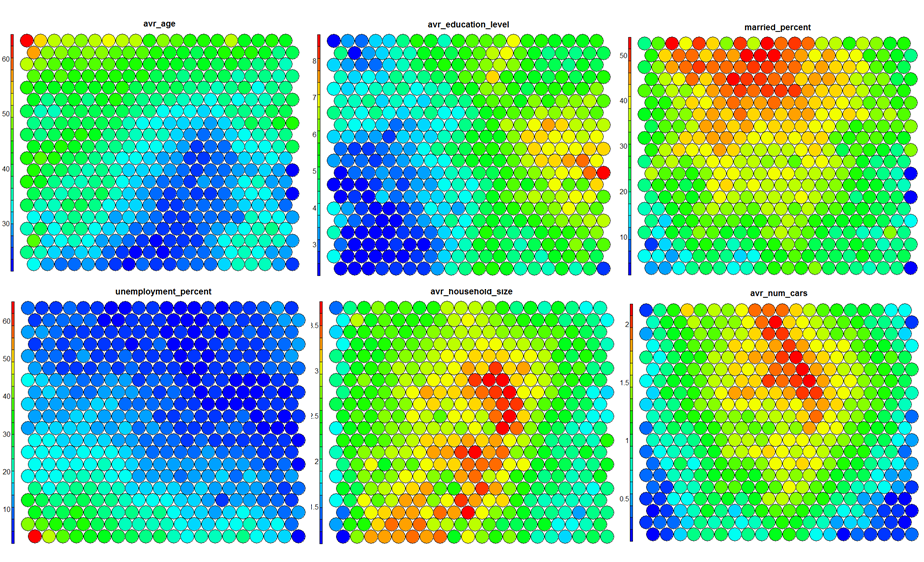
- Heatmaps
Heatmaps are perhaps the most important visualisation possible for Self-Organising Maps. The use of a weight space view as in (4) that tries to view all dimensions on the one diagram is unsuitable for a high-dimensional (>7 variable) SOM. A SOM heatmap allows the visualisation of the distribution of a single variable across the map. Typically, a SOM investigative process involves the creation of multiple heatmaps, and then the comparison of these heatmaps to identify interesting areas on the map. It is important to remember that the individual sample positions do not move from one visualisation to another, the map is simply coloured by different variables.
The default Kohonen heatmap is created by using the type “heatmap”, and then providing one of the variables from the set of node weights. In this case we visualise the average education level on the SOM.# Kohonen Heatmap creation plot(som_model, type = "property", property = getCodes(som_model)[,4], main=colnames(getCodes(som_model))[4], palette.name=coolBlueHotRed)
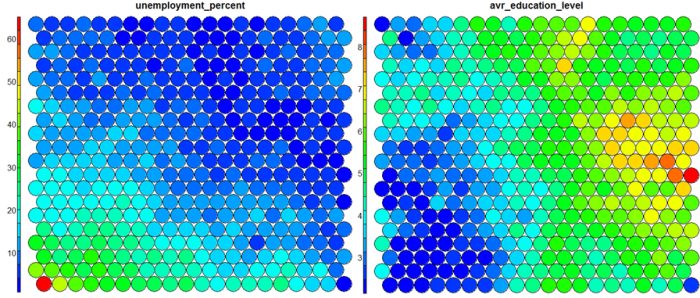
It should be noted that this default visualisation plots the normalised version of the variable of interest. A more intuitive and useful visualisation is of the variable prior to scaling, which involves some R trickery – using the aggregate function to regenerate the variable from the original training set and the SOM node/sample mappings. The result is scaled to the real values of the training variable (in this case, unemployment percent).
# Unscaled Heatmaps #define the variable to plot var_unscaled <- aggregate(as.numeric(data_train[,var]), by=list(som_model$unit.classif), FUN=mean, simplify=TRUE)[,2] plot(som_model, type = "property", property=var_unscaled, main=colnames(getCodes(som_model))[var], palette.name=coolBlueHotRed)
It is noteworthy that the heatmaps above immediately show an inverse relationship between unemployment percent and education level in the areas around Dublin. Further heatmaps, visualised side by side, can be used to build up a picture of the different areas and their characteristics.
Aside: Heatmaps with empty nodes in your SOM grid
In some cases, your SOM training may result in empty nodes in the SOM map. In this case, you won’t have a way to calculate mean values for these nodes in the “aggregate” line above when working out the unscaled version of the map. With a few additional lines, we can discover what nodes are missing from the som_model$unit.classif and replace these with NA values – this step will prevent empty nodes from distorting your heatmaps.# Plotting unscaled variables when you there are empty nodes in the SOM var_unscaled <- aggregate(as.numeric(data_train_raw[[variable]]), by=list(som_model$unit.classif), FUN=mean, simplify=TRUE) names(var_unscaled) <- c("Node", "Value") # Add in NA values for non-assigned nodes - first find missing nodes: missingNodes <- which(!(seq(1,nrow(som_model$codes)) %in% var_unscaled$Node)) # Add them to the unscaled variable data frame var_unscaled <- rbind(var_unscaled, data.frame(Node=missingNodes, Value=NA)) # order the resulting data frame var_unscaled <- var_unscaled[order(var_unscaled$Node),] # Now create the heat map only using the "Value" which is in the correct order. plot(som_model, type = "property", property=var_unscaled$Value, main=names(data_train)[var], palette.name=coolBlueHotRed)
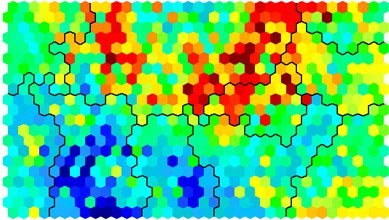
Clustering and Segmentation on top of Self-Organising Map
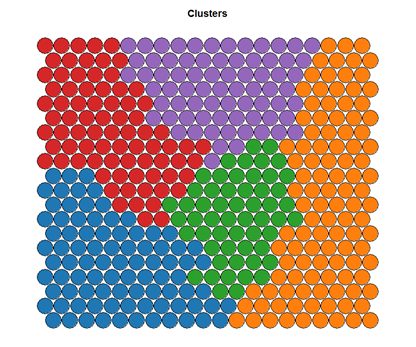
Clustering can be performed on the SOM nodes to isolate groups of samples with similar metrics. Manual identification of clusters is completed by exploring the heatmaps for a number of variables and drawing up a “story” about the different areas on the map. An estimate of the number of clusters that would be suitable can be ascertained using a kmeans algorithm and examing for an “elbow-point” in the plot of “within cluster sum of squares”. The Kohonen package documentation shows how a map can be clustered using hierachical clustering. The results of the clustering can be visualised using the SOM plot function again.
# Viewing WCSS for kmeans
mydata <- som_model$codes
wss <- (nrow(mydata)-1)*sum(apply(mydata,2,var))
for (i in 2:15) {
wss[i] <- sum(kmeans(mydata, centers=i)$withinss)
}
plot(wss)
# Visualising cluster results ## use hierarchical clustering to cluster the codebook vectors som_cluster <- cutree(hclust(dist(som_model$codes)), 6) # plot these results: plot(som_model, type="mapping", bgcol = pretty_palette[som_cluster], main = "Clusters") add.cluster.boundaries(som_model, som_cluster)
Ideally, the clusters found are contiguous on the map surface. However, this may not be the case, depending on the underlying distribution of variables. To obtain contiguous cluster, a hierachical clustering algorithm can be used that only combines nodes that are similar AND beside each other on the SOM grid. However, hierachical clustering usually suffices and any outlying points can be accounted for manually.
Mapping clusters back to original samples
When a clustering algorithm is applied as per the code example above, clusters are assigned to each of the nodes on the SOM map, rather than the original samples in the dataset. The key to assign labels to the original data is in using the som_cluster variable that maps nodes, with the som_model$unit.classif variable that maps data samples to nodes:
# get vector with cluster value for each original data sample cluster_assignment <- som_cluster[som_model$unit.classif] # for each of analysis, add the assignment as a column in the original data: data$cluster <- cluster_assignment
Use the statistics and distributions of the training variables within each cluster to build a meaningful picture of the cluster characteristics – an activity that is part art, part science! The clustering and visualisation procedure is typically an iterative process. Several SOMs are normally built before a suitable map is created. It is noteworthy that the majority of time used during the SOM development exercise will be in the visualisation of heatmaps and the determination of a good “story” that best explains the data variations.
Conclusions
Self-Organising Maps (SOMs) are another powerful tool to have in your data science repertoire. Advantages include: –
- Intuitive method to develop customer segmentation profiles.
- Relatively simple algorithm, easy to explain results to non-data scientists
- New data points can be mapped to trained model for predictive purposes.
Disadvantages include:
- Lack of parallelisation capabilities for VERY large data sets since the training data set is iterative
- It can be difficult to represent very many variables in two dimensional plane
- SOM training requires clean, numeric data which can be hard to get!
Please do explore the slides and code (2014-01 SOM Example code_release.zip) from the talk for more detail. Contact me if you there are any problems running the example code etc.



This is so awesome. Thanks for building. One question. When I try to use hierarchical clustering to cluster the codebook vectors, I run into an issue when referencing som_model$codes.
Error says that “(list) object cannot be coerced into type ‘double'”.
Any ideas?
Hi Eric, this is an issue with the new version of the Kohonen SOM library. Instead of som_model$codes, make sure to use getCodes(som_model) – that’ll fix up the issues!
Lovely. Thank you Shane.
🙂 apologies… Incredibly slow response time around this website!!
Consider using exploratory factor analysis instead of PCA, if you are interested in producing latent constructs that make sense strategically to your end user. You might give up a little bit of power in explaining variance, but you gain construct validity. It depends on whether you are going to go on to use these reduced factors in further work (e.g. behavior modeling, etc).
Here is a good guide. http://ww.personality-project.org/r/psych/HowTo/factor.pdf
Hi Shane,
I dont know how to find the total number of data in each node. How can I make these values appear on the map?i mean, when showing the plot i want the values on each node.
Thanks in advance
Hi I try run a example with R studio but it dont work . Problem is describe there : https://stackoverflow.com/questions/48251029/rstudio-object-not-found-kohonen-pack
Hi Caroline, it appears that you have no data loaded into your workspace in the variable “data”. Make sure to load a CSV file or other data source before running this script.
Hi. I try run example, but in clustering it writes this error : > wss <- (nrow(mydata)-1)*sum(apply(mydata,2,var))
Error in apply(mydata, 2, var) : dim(X) must have a positive length….. there are some rules what to put to apply ? or how to write wss ? My data are table 54×9, can be problem in size of matrix ?
Hi Shane. I try to use supersom as there are NAs in my data. The size of the data is 58×26, the size of the training data is 30×26. I got the error below when run the supersom. The size of the matrix should not be the problem?
Error in sample.int(length(x), size, replace, prob) : cannot take a sample larger than the population when ‘replace = FALSE’
It’s probably due to that the dimensions of the grid is larger than the sample size.
I got the same error and fixed it by adjust the grid to lower dimensions.
H Shane. This is great. After searching for so long, I finally found some good explanation. I have aquestion regarding the heatmap comparisions between unemplayment and education:
1) What are the axes?
2) What the nodes the plots? Are they locations or a set of people?
DO let me know. Anyone else is free to answer as well.
How do I map the above clusters back to original data. I believe segmentation of original data is whole objective.
Clustering used in above examples clusters the nodes(codes) in grid. However I wanted these clusters as an additional column in original data stating which record/row belongs to which cluster.
Please help me on this!
Hi Manish. This is a popular question, and a good one. I’ve added a new section to the clustering information above that describes the process. In essence, som_clusters maps nodes to cluster, and som_model$unit.classif maps samples to nodes. With these two, you can map your new cluster values to the original data samples – Good luck!
Hi. Great tutorial. I try some SOM map by myself , but I dont know how to find numerical result of SOM map. Or it is not possible ? Details of my question : https://stackoverflow.com/questions/49552721/som-map-kohonen-package-numerical-result
The plot command to colorize the clustered nodes using pretty_palette does not work. pretty_palette() takes one integer as an argument where the som_cluster has more than one element. It also does not use brackets. Is there more to this command, or am I using an incorrect pretty_palette?
Apologies, I should have made this clearer in the post. On the Github repository, I define a palette for colouring the map:
# Colour palette definition
pretty_palette <- c("#1f77b4", '#ff7f0e', '#2ca02c', '#d62728', '#9467bd', '#8c564b', '#e377c2')
Thanks! I also found a way to make the code work by adding “(6)” between pretty_palette and [som_cluster]:
plot(som_model, type=”mapping”, bgcol = pretty_palette(6)[som_cluster], main = “Clusters”)
Hello Shane, great article! Just wondering how to make these visualizations interactive? I mean, like in a dashboard say with PowerBI? I researched and found although ggplot2 and plotly can give wonderful control over visualizations, they are incompatible with the Kohonen package in R?
How to can these graphs interactive?? Anyone???
I am also looking for similar answer. If you/anyone have found please let me know.
Tough one guys – there is some interactivity for clicking on individual nodes if you look at the documentation for kohonen.plot. Outside of this, there’s a closed source tool called Viscovery that might be worth a look, or you can look at this site: https://www.visualcinnamon.com/2013/07/self-organizing-maps-creating-hexagonal which may be useful, but difficult unless you are familiar with javascript.
@Shaelynn, thank you.
Thanks Shane. Yes, I was thinking the same; moving it to JS along with Shiny.
@Irshad, I have built a dashboard with PowerBI. Use the R script from visualizations in PowerBI, simply paste the R codes in the widget and you’re good to go.
Check out the screenshot >>
https://www.linkedin.com/feed/update/urn:li:activity:6407988285628612608/?commentUrn=urn%3Ali%3Acomment%3A(activity%3A6407988285628612608%2C6408346666373615616)
Thank you @Rupsayar. Will surely try that.
I noticed (correct me if I am wrong) those maps in your linked in link were showing standardized scales, it would be more intuitive if you bring them back to original scale.
@Shane, I tried to plot the distribution of features for a subset of observations in a same cluster obtained using hierarchical clustering. I was expecting the distribution which I see through histogram should be same as obtained by SOM heatmap. I saw that histogram is telling me the different story as compared to the heatmap. As the heatmap is drawn on weight vectors, shouldn’t the histogram of a feature (for observation in a particular cluster) and heatmap of of that cluster interprete same results. In my case, it is not happening. How to make sure both match?
This is resolved. Thank you.
I am finding one things confusing. As SOM already helps to reduce the dimensions and cluster neighbouring nodes together. Why on the top of nodes hierarchical clustering is applied?
How is that different from applying hierarchical clustering on the original data (without applying SOM on the data)?
I applied both of these techniques on a 2-dimensional data and got similar results. What is whole point of SOM? Why can’t we simply skip SOM? Is preserving the topological distances is only the advantage with SOM? Why topological distances are important? As with clustering as well I am getting similar observation (with the help of distances) in the same cluster.
Hi Artiga. I think it’s best to think of SOM as a visualisation technique rather than a dimensionality reduction technique. The nodes are clustered to help the user to discern between broadly similar node groupings. Technically, you are clustering the results of a clustering – i.e. the nodes themselves are similar to small clusters. You will get similar, and potentially better, clustering results from applying hierarchical clustering on the data directly. My advice is to use SOM technique as a visual aid for presentation and data exploration.
Thank you for the reply. This leads to couple of doubts:
1. In SOM similar (same color) nodes will be closer to each other forming clusters. And the colors of the neighbour nodes will be same. Then why do we need clustering again over these nodes?
2. On what basis you are saying that clustering results obtained by applying hierarchical clustering directly on the data will be potentially better? Is there way I can find out which clustering is better in this case?
Hi Shane,
How can I get the row names (individual ) to plot inside my heat map? In the well known SOM heat map for world poverty the country names are printed inside the nodes. Can you help, please?
Excellent explanation. Loved it.
Hi.. Following code cant find data_train_raw and variables in it
# Plotting unscaled variables when you there are empty nodes in the SOM
var_unscaled <- aggregate(as.numeric(data_train_raw[[variable]]),
Dear Shane Lynn,
I am trying to run the som_model following your paths but I cannot understand why everytime that I run som_model lines then plot it with type=count, I have a different plot everytime.
My database has 323 lines and 14 variables. The code that I am using is:
set.seed(100)
som_grid <- somgrid(xdim = 5, ydim=5, topo="hexagonal")
grille <-som(NoNAData1Scale,som_grid,rlen=100,keep.data=TRUE)
plot(grille,type="count")
Hi Aurore, this shouldn’t be the case – can you run this line by line to make sure that the seed is being set correctly – the SOM algorithm is stochastic, but if the seed is set, you should get the same results each time. Are there any steps before this that may be reordering your data?
Hello.
Question 1:
Can this technique be used with time series as well?
For example, I would have 20 station data. Each station would have, lets say 100 observation per day, And there are 40 days. So the dataset would be 20x100x40.
Question 2:
A simpler one would be maybe hundreds of time series with different length. I would fill those ’empty’ parts with NA. How would I apply this technique to this dataset?
Hi Muhammad, thanks for getting in touch. This will work with time series – you’ll need to decide if you are segmenting days, or stations -i.e asking – what type of different days are there? -or- what type of different stations are there? I imagine days will be a better result. So you would organise the data with each day being one row, and summary stats from the time series from each station as columns. Or the entire time series if you’d like – but this will be very wide.
The SOM algorithm as is will not work with missing values -you should fill these with mean or median values as necessary.
Lets try the simplest one first.
1 Station
100 days of observation.
Each day has 24 observation.
Yes I prefer the entire time series for the analysis. Like grouping days when an ‘event’ peaks in the morning, or it peaks some other time, or no ‘event’ at all. In this case a summary of the time series will not do any good.
In actuality, I would like to apply it differently. One example is that the time series is actually an area. Instead of lets say wind recorded in one station, its wind field from reanalysis. From what I’m reading from the documentation and example, its not possible for analysing area data?
The next example is instead of a daily 24 hours observation, its a calculated event with different lengths. Which you suggested to use mean/median instead of NA to fill as necessary. This will be hard as some event can be quite long, days long and some event are just less than one day.
The description of supersom {kohonen} 3.0.7 says as below. That means what I’m planning should be achievable isn’t it? Just have to get into it and try it step by step. And NA’s are allowed.
“A supersom is an extension of self-organising maps (SOMs) to multiple data layers, possibly with different numbers and different types of variables (though equal numbers of objects). NAs are allowed. A weighted distance over all layers is calculated to determine the winning units during training. Functions som and xyf are simply wrappers for supersoms with one and two layers, respectively. Function bdk is deprecated.”
Hi Shane!
Thank you so much for the post. It is very helpful!
I have just a question.
I would like to use SOM and I have a dataset with 27 expenditure’s variables expressed in QUINTILES. So, each variable can assume the values 0,1,2,3,4,5.
I know that, in case of categorical attributes, it is necessary to transform each categorical attribute into a set of binary attributes 0-1 before the SOM.
In my specific case, I have to transform my entire dataset in binary values for each value of the variable (0:6) or, considering that the values are quintiles of expenditure, I can work with the original data?
Thanks in advance!
Simona
can I use serial time data with SOM
Thanks for sharing the work. I want to know how to calculate the quantization error and topological error in SOM network.
You must add double bracket and the number of your som map that you want to cluster. For example: som_model$codes[[1]]
[…] saber más:Representation of data using a Kohonen map, followed by a cluster analysis. Self-Organising Maps for Customer Segmentation using R.Los mapas auto-organizados de Kohonen (SOM).Kohonen package | R […]
[…] [4] Much direction for structuring this tutorial comes from https://www.shanelynn.ie/self-organising-maps-for-customer-segmentation-using-r/ […]
[…] [4] Much direction for structuring this tutorial comes from https://www.shanelynn.ie/self-organising-maps-for-customer-segmentation-using-r/ […]
Hi Shane,
if I want to create inference using SOM built in R then how to do it? do you have any idea?
HI, i have an issue with this command;
wss <- (nrow(mydata)-1)*sum(apply(mydata,2,var))
**Error in apply(mydata, 2, var) : dim(X) must have a positive length
Any suggestions to solve it?
Thanks in advance