Self-Organising Maps
Self-Organising Maps (SOMs) are an unsupervised data visualisation technique that can be used to visualise high-dimensional data sets in lower (typically 2) dimensional representations. In this post, we examine the use of R to create a SOM for customer segmentation. The figures shown here used use the 2011 Irish Census information for the greater Dublin area as an example data set. This work is based on a talk given to the Dublin R Users group in January 2014.
Note: This post has been updated for changes in the Kohonen API and R 3.2 in 2017.
If you are keen to get down to business:
The slides from a talk on this subject that I gave to the Dublin R Users group in January 2014 are available here (code is in the slides is *slightly* out of date now)
The updated code and data for the SOM Dublin Census data is available in this GitHub repository.
The code for the Dublin Census data example is available for download from here. (zip file containing code and data – filesize 25MB)
SOMs were first described by Teuvo Kohonen in Finland in 1982, and Kohonen’s work in this space has made him the most cited Finnish scientist in the world. Typically, visualisations of SOMs are colourful 2D diagrams of ordered hexagonal nodes.
The SOM Grid
SOM visualisation are made up of multiple “nodes”. Each node vector has:
- A fixed position on the SOM grid
- A weight vector of the same dimension as the input space. (e.g. if your input data represented people, it may have variables “age”, “sex”, “height” and “weight”, each node on the grid will also have values for these variables)
- Associated samples from the input data. Each sample in the input space is “mapped” or “linked” to a node on the map grid. One node can represent several input samples.
The key feature to SOMs is that the topological features of the original input data are preserved on the map. What this means is that similar input samples (where similarity is defined in terms of the input variables (age, sex, height, weight)) are placed close together on the SOM grid. For example, all 55 year old females that are appoximately 1.6m in height will be mapped to nodes in the same area of the grid. Taller and smaller people will be mapped elsewhere, taking all variables into account. Tall heavy males will be closer on the map to tall heavy females than small light males as they are more “similar”.
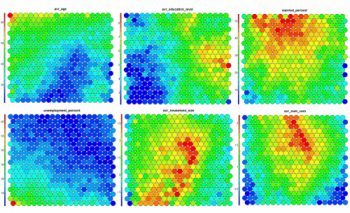
SOM Heatmaps
Typical SOM visualisations are of “heatmaps”. A heatmap shows the distribution of a variable across the SOM. If we imagine our SOM as a room full of people that we are looking down upon, and we were to get each person in the room to hold up a coloured card that represents their age – the result would be a SOM heatmap. People of similar ages would, ideally, be aggregated in the same area. The same can be repeated for age, weight, etc. Visualisation of different heatmaps allows one to explore the relationship between the input variables.
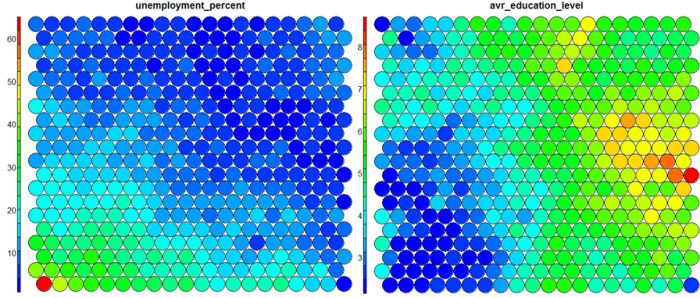
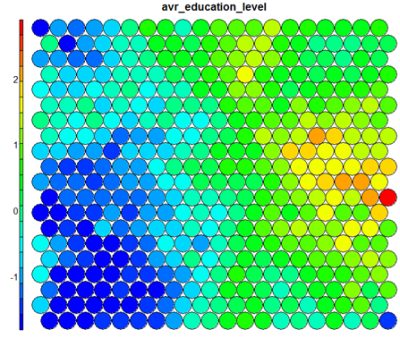
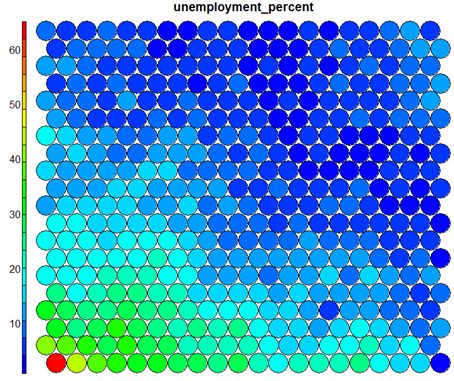
The figure below demonstrates the relationship between average education level and unemployment percentage using two heatmaps. The SOM for these diagrams was generated using areas around Ireland as samples.
SOM Algorithm
The algorithm to produce a SOM from a sample data set can be summarised as follows:
- Select the size and type of the map. The shape can be hexagonal or square, depending on the shape of the nodes your require. Typically, hexagonal grids are preferred since each node then has 6 immediate neighbours.
- Initialise all node weight vectors randomly.
- Choose a random data point from training data and present it to the SOM.
- Find the “Best Matching Unit” (BMU) in the map – the most similar node. Similarity is calculated using the Euclidean distance formula.
- Determine the nodes within the “neighbourhood” of the BMU.
– The size of the neighbourhood decreases with each iteration. - Adjust weights of nodes in the BMU neighbourhood towards the chosen datapoint.
– The learning rate decreases with each iteration.
– The magnitude of the adjustment is proportional to the proximity of the node to the BMU. - Repeat Steps 2-5 for N iterations / convergence.
Sample equations for each of the parameters described here are given on Slideshare.
SOMs in R
Training
The “kohonen” package is a well-documented package in R that facilitates the creation and visualisation of SOMs. To start, you will only require knowledge of a small number of key functions, the general process in R is as follows (see the presentation slides for further details):
# Creating Self-organising maps in R # Load the kohonen package require(kohonen) # Create a training data set (rows are samples, columns are variables # Here I am selecting a subset of my variables available in "data" data_train <- data[, c(2,4,5,8)] # Change the data frame with training data to a matrix # Also center and scale all variables to give them equal importance during # the SOM training process. data_train_matrix <- as.matrix(scale(data_train)) # Create the SOM Grid - you generally have to specify the size of the # training grid prior to training the SOM. Hexagonal and Circular # topologies are possible som_grid <- somgrid(xdim = 20, ydim=20, topo="hexagonal") # Finally, train the SOM, options for the number of iterations, # the learning rates, and the neighbourhood are available som_model <- som(data_train_matrix, grid=som_grid, rlen=500, alpha=c(0.05,0.01), keep.data = TRUE )
Visualisation
The kohonen.plot function is used to visualise the quality of your generated SOM and to explore the relationships between the variables in your data set. There are a number different plot types available. Understanding the use of each is key to exploring your SOM and discovering relationships in your data.
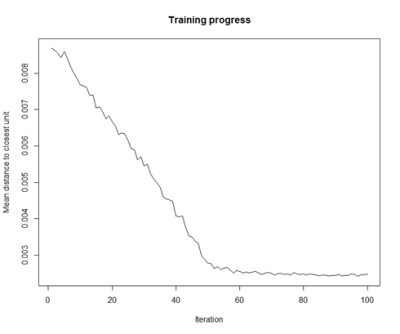
- Training Progress:
As the SOM training iterations progress, the distance from each node’s weights to the samples represented by that node is reduced. Ideally, this distance should reach a minimum plateau. This plot option shows the progress over time. If the curve is continually decreasing, more iterations are required.#Training progress for SOM plot(som_model, type="changes")
- Node Counts
The Kohonen packages allows us to visualise the count of how many samples are mapped to each node on the map. This metric can be used as a measure of map quality – ideally the sample distribution is relatively uniform. Large values in some map areas suggests that a larger map would be benificial. Empty nodes indicate that your map size is too big for the number of samples. Aim for at least 5-10 samples per node when choosing map size.#Node count plot plot(som_model, type="count", main="Node Counts")
- Neighbour Distance
Often referred to as the “U-Matrix”, this visualisation is of the distance between each node and its neighbours. Typically viewed with a grayscale palette, areas of low neighbour distance indicate groups of nodes that are similar. Areas with large distances indicate the nodes are much more dissimilar – and indicate natural boundaries between node clusters. The U-Matrix can be used to identify clusters within the SOM map.# U-matrix visualisation plot(som_model, type="dist.neighbours", main = "SOM neighbour distances")
- Codes / Weight vectors
Thenode weight vectors, or “codes”, are made up of normalised values of the original variables used to generate the SOM. Each node’s weight vector is representative / similar of the samples mapped to that node. By visualising the weight vectors across the map, we can see patterns in the distribution of samples and variables. The default visualisation of the weight vectors is a “fan diagram”, where individual fan representations of the magnitude of each variable in the weight vector is shown for each node. Other represenations are available, see the kohonen plot documentation for details.# Weight Vector View plot(som_model, type="codes")
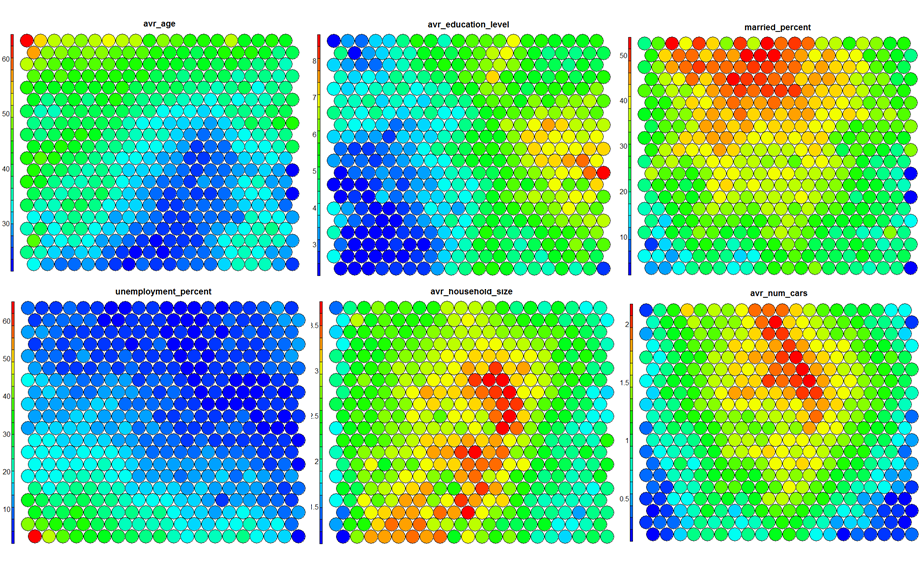
- Heatmaps
Heatmaps are perhaps the most important visualisation possible for Self-Organising Maps. The use of a weight space view as in (4) that tries to view all dimensions on the one diagram is unsuitable for a high-dimensional (>7 variable) SOM. A SOM heatmap allows the visualisation of the distribution of a single variable across the map. Typically, a SOM investigative process involves the creation of multiple heatmaps, and then the comparison of these heatmaps to identify interesting areas on the map. It is important to remember that the individual sample positions do not move from one visualisation to another, the map is simply coloured by different variables.
The default Kohonen heatmap is created by using the type “heatmap”, and then providing one of the variables from the set of node weights. In this case we visualise the average education level on the SOM.# Kohonen Heatmap creation plot(som_model, type = "property", property = getCodes(som_model)[,4], main=colnames(getCodes(som_model))[4], palette.name=coolBlueHotRed)
It should be noted that this default visualisation plots the normalised version of the variable of interest. A more intuitive and useful visualisation is of the variable prior to scaling, which involves some R trickery – using the aggregate function to regenerate the variable from the original training set and the SOM node/sample mappings. The result is scaled to the real values of the training variable (in this case, unemployment percent).
# Unscaled Heatmaps #define the variable to plot var_unscaled <- aggregate(as.numeric(data_train[,var]), by=list(som_model$unit.classif), FUN=mean, simplify=TRUE)[,2] plot(som_model, type = "property", property=var_unscaled, main=colnames(getCodes(som_model))[var], palette.name=coolBlueHotRed)
It is noteworthy that the heatmaps above immediately show an inverse relationship between unemployment percent and education level in the areas around Dublin. Further heatmaps, visualised side by side, can be used to build up a picture of the different areas and their characteristics.
Aside: Heatmaps with empty nodes in your SOM grid
In some cases, your SOM training may result in empty nodes in the SOM map. In this case, you won’t have a way to calculate mean values for these nodes in the “aggregate” line above when working out the unscaled version of the map. With a few additional lines, we can discover what nodes are missing from the som_model$unit.classif and replace these with NA values – this step will prevent empty nodes from distorting your heatmaps.# Plotting unscaled variables when you there are empty nodes in the SOM var_unscaled <- aggregate(as.numeric(data_train_raw[[variable]]), by=list(som_model$unit.classif), FUN=mean, simplify=TRUE) names(var_unscaled) <- c("Node", "Value") # Add in NA values for non-assigned nodes - first find missing nodes: missingNodes <- which(!(seq(1,nrow(som_model$codes)) %in% var_unscaled$Node)) # Add them to the unscaled variable data frame var_unscaled <- rbind(var_unscaled, data.frame(Node=missingNodes, Value=NA)) # order the resulting data frame var_unscaled <- var_unscaled[order(var_unscaled$Node),] # Now create the heat map only using the "Value" which is in the correct order. plot(som_model, type = "property", property=var_unscaled$Value, main=names(data_train)[var], palette.name=coolBlueHotRed)
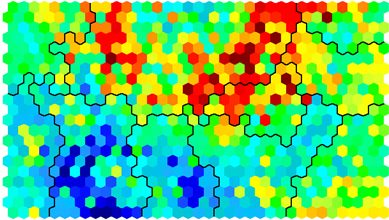
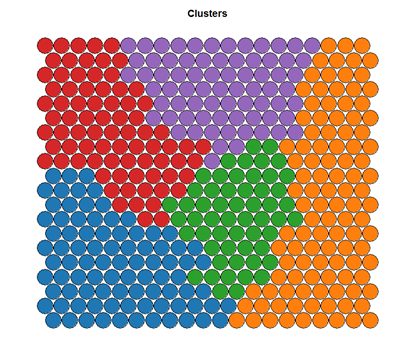
Clustering and Segmentation on top of Self-Organising Map
Clustering can be performed on the SOM nodes to isolate groups of samples with similar metrics. Manual identification of clusters is completed by exploring the heatmaps for a number of variables and drawing up a “story” about the different areas on the map. An estimate of the number of clusters that would be suitable can be ascertained using a kmeans algorithm and examing for an “elbow-point” in the plot of “within cluster sum of squares”. The Kohonen package documentation shows how a map can be clustered using hierachical clustering. The results of the clustering can be visualised using the SOM plot function again.
# Viewing WCSS for kmeans
mydata <- som_model$codes
wss <- (nrow(mydata)-1)*sum(apply(mydata,2,var))
for (i in 2:15) {
wss[i] <- sum(kmeans(mydata, centers=i)$withinss)
}
plot(wss)
# Visualising cluster results ## use hierarchical clustering to cluster the codebook vectors som_cluster <- cutree(hclust(dist(som_model$codes)), 6) # plot these results: plot(som_model, type="mapping", bgcol = pretty_palette[som_cluster], main = "Clusters") add.cluster.boundaries(som_model, som_cluster)
Ideally, the clusters found are contiguous on the map surface. However, this may not be the case, depending on the underlying distribution of variables. To obtain contiguous cluster, a hierachical clustering algorithm can be used that only combines nodes that are similar AND beside each other on the SOM grid. However, hierachical clustering usually suffices and any outlying points can be accounted for manually.
Mapping clusters back to original samples
When a clustering algorithm is applied as per the code example above, clusters are assigned to each of the nodes on the SOM map, rather than the original samples in the dataset. The key to assign labels to the original data is in using the som_cluster variable that maps nodes, with the som_model$unit.classif variable that maps data samples to nodes:
# get vector with cluster value for each original data sample cluster_assignment <- som_cluster[som_model$unit.classif] # for each of analysis, add the assignment as a column in the original data: data$cluster <- cluster_assignment
Use the statistics and distributions of the training variables within each cluster to build a meaningful picture of the cluster characteristics – an activity that is part art, part science! The clustering and visualisation procedure is typically an iterative process. Several SOMs are normally built before a suitable map is created. It is noteworthy that the majority of time used during the SOM development exercise will be in the visualisation of heatmaps and the determination of a good “story” that best explains the data variations.
Conclusions
Self-Organising Maps (SOMs) are another powerful tool to have in your data science repertoire. Advantages include: –
- Intuitive method to develop customer segmentation profiles.
- Relatively simple algorithm, easy to explain results to non-data scientists
- New data points can be mapped to trained model for predictive purposes.
Disadvantages include:
- Lack of parallelisation capabilities for VERY large data sets since the training data set is iterative
- It can be difficult to represent very many variables in two dimensional plane
- SOM training requires clean, numeric data which can be hard to get!
Please do explore the slides and code (2014-01 SOM Example code_release.zip) from the talk for more detail. Contact me if you there are any problems running the example code etc.



Hello Shane:
Great work!!!! I loved your work, although I’m having a problem with your last code, my R package cant find the Pretty_palette colour scheme and I can’t find it in your code, nor I now how to replace it by other code, can you help me?
Derek, thanks for reading. And even better to get feedback. There should be a definition for the palette in the code – but if not – just define using:
# Colour palette definition
pretty_palette <- c("#1f77b4", '#ff7f0e', '#2ca02c', '#d62728', '#9467bd', '#8c564b', '#e377c2') You'll find the colours quite similar to those used in Tableau vizualisations. 🙂
Hi Shane
Thanks for sharing. Excellent for someone who’s learning the ropes of SOM clustering in R. I notice that in the slides, you used a different function (clusterSOM) for defining the clusters, whereas in the supplementary material, hierarchical cluster function hclust is used. Which clustering technique is used in clusterSOM (it is not defined in the provided material)?
Thanks once again
Hey Gorden. The clusterSom() function that was referenced on the slides used a form of hierarchical clustering that was altered to only combine nodes that are adjacent on the map. This leads to clusters that are contiguous on the map area, which is desirable. However, unfortunately the code for that bit is not mine, so I can’t release it on the site! But with a little tinkering, you might be able to replicate this functionality. Glad you enjoyed the post.
Thanks Shane.
Hi Gorden, Did you ever manage to write up the function? I would love to get a copy of it to save me time writing it.
Great post Shane!
Nice and easy to follow, though I do have one question. How can I get a listing of all GEOGIDs in a particular cluster or node?
Hey June. Thanks for reading. Looking for all of the GEOGIDs for a single cluster will require the use of the ‘som_model$unit.classif’ and the ‘som_cluster’ variables. You can assign a ‘cluster’ variable in the original data frame using the line:
data$cluster <- som_cluster[som_model$unit.classif]And along with that, you can identify the node that each sample belongs to using:
data$node <- som_model$unit.classifTo identify the node numbers - have a look at the kohonen.identify function - run it like
identify(som_model)and then click on the map.Absolutely fabulous work specially the explanation and presentation. I have been working on almost the same problem for identifying generic trends for Indian economic data and found your work most useful.
Quick question: While clustering, I am getting very density of values for one cluster only. Had tried changing the som model parameters but did not find much change. Could you recommend from your experience any steps to handle this bias?
Thanks a lot!!
Hey Parth, I’m glad that you found the post useful. I’m not sure what you mean by “very density of values for one cluster only”. However, if you find that one particular node in the map is being assigned a much higher number of samples than usual… there are two solutions: 1.) This is ok if the node “quality” is not unusually high. Have a look at the samples in the node and ensure they are all similar – this may just be a property of your data. 2.) Increase the size of your map overall so that there is enough “space” for the samples to spread out more. However, this may end up with you having a number of empty nodes in your map.
Outstanding work on SOM. Im relatively new to R although experienced with SOM. I “grew-up” on Viscovery, but I currently I dont have the budget so I am looking for whats available and I found your blog. I am going straigh to the point: So I have a dummy matrix of flagged data similar to the following: X0 X1 X0.1 X0.2 X1.1 X0.3 X0.4 X1.2 1 1 0 0 1 0 0 1 0 2 1 0 0 1 0 0 1 0 3 1 0 0 0 1 0 0 1 4 1 0 0 0 1 0 0 1 5 1 0 0 0 1 0 0 1 6 1 0 0 0 1 0 0 1 7 1 0 0 0 1 0 0 1 8 1 0 0 0 1 0 0 1 9 1 0 0 0 1 0 0 1 10 1 0 0 0 1 0 0 1 11 1 0 0 0 1 0 0 1 12 1 0 0 0 1 0 0 1 13 1 0 0 0 1 0 0 1 14 1 0 0 0 1 0 0 1 15 1 0 0 0 1 0 0 1 16 0 1 0 1 0 0 1 0 17 0 1 0 1 0 0 1 0 18 0 1 0 1 0 0 1 0 19 0 1 0 1 0 0 1 0 20 0 1 0 1 0 0 1 0 21 0 1 0 1 0 0 1 0 22 0 1 0 1 0 0 1 0 23 0 1 0 1 0 0 1 I seem to be doing wrong something on this step: som_model <- som(data_train_matrix, grid=som_grid, rlen=100, alpha=c(0.05,0.01), keep.data = TRUE, n.hood=“circular” ) In one computer I dont get any error.… Read more »
Hey Carlos – it sounds like there is something weird with the sizes of your data sets – but I can’t seem to replicate the problem here. Can you post a fully functional piece of code that reproduces the problem and I’ll have a look!?
How to get topological error, quantization error, trustworthiness and hit histogram?
I’d like to discuss about kohonen algorithm applied to financial ratios. Preprocessing technique, more then 10 dimensions etc. My mail: mariozupansystems@gmail.com
I was able to make it work 🙂
Lets be in touch, whats the best linkedin profile to contact you?
I can’t get the same values of quantization and topographic errors with Matlab somtoolbox and above R code.
And Carlos – my linkedin profile is up at the top of the page!
Mario, that would be expected – the SOM algorithm is stochastic in nature – so technically you will end up with a different set of values each time that you create a map. Are the values very different?
Great Tute! Just one question about plotting the different variables on the map ,i.e.
var <- 2 #define the variable to plot
var_unscaled <- aggregate(as.numeric(data_train[,var]), by=list(som_model$unit.classif), FUN=mean, simplify=TRUE)[,2]
plot(som_model, type = "property", property=var_unscaled, main=names(data_train)[var], palette.name=coolBlueHotRed)
In my data set I have 5 variables with about 2755 observations that roughly follow an exponential distribution but when ever I use that section of code I get a Warning message:
In bgcolors[!is.na(showcolors)] <- bgcol[showcolors[!is.na(showcolors)]] :
number of items to replace is not a multiple of replacement length.
I think this is because the length of var_unscaled is only 789 where as the length of all the other vectors is 2755. Any idea's?
Hey James, sorry for the late reply – i’ve been missing a few notifications from the site. My bet here is that you have a strange numerical contraint on the column in question – does it have a std. dev. of 0 or some missing values? also, make sure that som_model$unit.classif is the correct length and has the same number of unique values as there are nodes in the map. Hope this helps!
Very good post!
I have a question. My train set have 784 columns and more one called label. After clustering, how do I do to export for each row train set, the label found in the clustering (labels 0 to 9, i.e. clusters 0 to 9)
For example:
Train set
row | Label,datas
#1 | 0 ,000100101010101101101…
#2 | 0 ,111010101101010101010…
#3 | 2 ,110101000010101010001…
#4 | 5 ,000010101000100101010…
…
The repost I need after clustering
row | cluster
#1 | 0
#2 | 0
#3 | 2
#4 | 5
…
Hey Filran, sorry for the delay. If it’s the cluster number that you are looking for you should be able to find it under “som_cluster”.
From fan diagram we can see distribution of variables across map. But, how can we know “where is the area (for example) with highest average ages” ?
Hey Maulina, Good question – best off to do this visually with the fan diagram, or better still, to produce a heat map of ages and look for concentration of ages. However, remember that if you didn’t use “age” to actually produce the segmentation, they may not be clustered together. The mapping back to the actual electoral areas is found in som_model$unit.classif.
Great work and thanks for sharing Shane.
I am trying to use the data produced by R to create an interactive plot in d3. in particular I would like to be able to zoom over each node to see which sample it contains.
I managed to locate all the data I need except the color of the nodes produced by the plot function. Is there a way to “extract” the color of each node in a vector?
Hey Ulrich. Great if you get something working in d3 – its a difficult library – i would love to see your results. The colors should be contained in the ‘pretty_palette’ variable. To find the colour of a single node, I think it would be something like: pretty_palette[som_cluster[node_in_question]]
Let me know how you get on!
Great post…wish I had seen it earlier, but just starting to learn R.
One question – how did you generate the area charts on pages 34/35 of the presentation showing cluster vs population for each criteria (e.g .age, unemployment, etc…)
Thanks!
Hi Shane,
I am just starting to use this analysis in R so thank you for posting this, it has been very helpful.
There is a comment above about the results being slightly different every time you create the map.
Do you know of a way to go back to exactly the same map in R the next time you plot the model (perhaps you can export the model in some way then reload it later)?
I am trying to map different features to my map to assess how they cluster, but because I have a lot of features to assess and the way they are classified may change, it would be very helpful to be able to reproduce a given map at a later date, as even slight changes in the layout may affect the reliability of conclusions that can be drawn from the analysis.
I would be very grateful for any suggestions! Thanks.
Hey shane, I’m sorry I didn’t see your answer to me about topographic and quantization errors, but this is less important to me right now. Results are not so different. Right now I’m curious about Average Silhouette results. I got 0,21 index which is very poor results according to some explanations of index. I tried this:
cell<-som_model$unit.classif
data_train$cluster<-som_cluster[cell]
dissE <- daisy(data_train)
dE2 <- dissE^2
sk2 <- silhouette(data_train$klasteri, dE2)
windows()
plot(sk2)
One more thing. You wrote some disadvantages of SOM. What if you have 30 variables in your dataset? What clustering alghorithm you will use as an replacement for SOM?
Very nicely written code!!! I would like to use your code in a class that I teach on neural networks. I normally include some examples from public domain. The class will have references to your work and this blog. Please let me know if you have any additional licenses on your code and if it is in the public domain.
BTW, I tried your contact page – does not show up on mozilla.
Hi Surya – no problem to include the code in a teaching class – its a good way to get people interested in SOMs and machine learning. Code is pretty much public domain!
Very nice introduction, thanks a lot.
Is there an easy way to add the cluster number of each observation in the original dataset? i am not able to see whether they are stored somewhere. best M.
Hi Marco – its been a good while since I wrote the code, but i think that you should be able to get the cluster number in the original dataset using:
data$cluster <- som_cluster[som_model$unit.classif]
Shane,
Love this page – was incredibly helpful in building a SOM for a project that I am working on and so far it has been working great. However, I know that we are eventually going to need to use the SOM model to run some predictions on additional data and I can’t seem to figure out how the predict function is supposed to work correctly. I assume that the new data will need to be converted to a matrix using the same process as the original data? And, mostly I think I’m getting hung up on the “trainY” argument. I can’t figure out what that is supposed to look like and the examples I have found online are not very helpful or informative. Do you have any resources or insight on how to run this last step in the process?
Thanks!
Hi Shane,thanks very much for your outstanding work. I want to use your code in my work, but I met some problem, could you please help me some favors?To my files, the .CVS and .shape were organized the same, and I have do the standardization and deal with the incomplete manually, therefore I jumped into the train parts:
data_train <- data_raw[, c(2,3,4,5,6,7,8,9,10)], but I met a problem in after the step"names(data_train_matrix) <- names(data_train)"
Error in names(data_train_matrix) <- names(data_train) : the length of the name in"names" should be the same as the length of the name in vector.
And if I change the training like: data_train <- data_raw[, c(2)], and the errors show as: Error in sample.int(length(x), size, replace, prob) :
'replace = FALSE', the sample can not be bigger than data.
Could you give me some advice about these problem, I think that I did not quite understand the step of choosing sample, and my data including 10 variables and 4000 polygons, how I can choose the sample properly to do the further SOM analysis?
Thanks again for your great job, I am looking forward to your reply. Cheers
Dear shane,
thanks for this nice introduction, I would be interested in the clusterSom() function to get contiguous clusters. Would it be possible to get a hint on this?
Cheers
Florian
Awesome work Shane! Thanks for sharing. here is something i found on the net on how to calculate the number of neurons to use
topology=function(data)
{
#Determina, para lattice hexagonal, el número de neuronas (munits) y su disposición (msize)
D=data
# munits: número de hexágonos
# dlen: número de sujetos
dlen=dim(data)[1]
dim=dim(data)[2]
munits=ceiling(5*dlen^0.5) # Formula Heurística matlab
#munits=100
#size=c(round(sqrt(munits)),round(munits/(round(sqrt(munits)))))
A=matrix(Inf,nrow=dim,ncol=dim)
for (i in 1:dim)
{
D[,i]=D[,i]-mean(D[is.finite(D[,i]),i])
}
for (i in 1:dim){
for (j in i:dim){
c=D[,i]*D[,j]
c=c[is.finite(c)];
A[i,j]=sum(c)/length(c)
A[j,i]=A[i,j]
}
}
VS=eigen(A)
eigval=sort(VS$values)
if (eigval[length(eigval)]==0 | eigval[length(eigval)-1]*munits<eigval[length(eigval)]){
ratio=1
}else{
ratio=sqrt(eigval[length(eigval)]/eigval[length(eigval)-1])}
size1=min(munits,round(sqrt(munits/ratio*sqrt(0.75))))
size2=round(munits/size1)
return(list(munits=munits,msize=sort(c(size1,size2),decreasing=TRUE)))
}
Hi Shane. Nicely written and well explained article. Can you share the code for plotting density plot with population to visualize cluster details? I see them on the slides but there is no code associated to it. Many thanks. Zee
Hi Zeehasham, just thought i’d replicate the email here- plot was made up using ggplot2 library with a geom_density() plot and alpha set to 0.6 or so. Use facet_grid() to get the 4 plots. There’s a bit of data reorganisation to be completed first. I’m going to write a separate post on how to interrogate clusters etc.
Shane, very clear and thorough analysis. A couple of questions for you – Are there any rules of guidelines you follow when choosing the size of the map (ie why did you settle on a 20×20 map)? Also, in this example you do not have any empty nodes in the map. Is having empty nodes in the map acceptable or should they be avoided?
Thanks Sean! Good to hear that you made use of it. Unfortunately choosing the map size is more art than science! I experimented with map sizes starting with 10×10 and essentially used the node density plots to find a map size where the samples were relatively well spread around the map. When the map is too small, you usually find a huge number of samples in one corner, and when too big there’s usually a large number of empty nodes. It is possible with some data sets that this balance will be hard to find, and in such case, I would look at some data transformations to reduce any outliers or scale effects on variables. Hope this helps, Shane.
Hi Shane,Great work and thanks for sharing. One question for you:When I used plot(data,type=”mapping”) ,and my code is :
##data.som <- som(data =mydata, grid = somgrid(som.x, som.y, "hexagonal"), rlen = 100, toroidal=TRUE)
##plot(data.som, type="mapping",palette.name=colorRampPalette(brewer.pal(8,"Blues")))
But it went wrong,just like this:
##Error in polygon(X_vec, Y_vec, border = "black", col = bg) : object 'bgcolors' not found
So,what does that mean? And any suggestion will be highly appreciated.
Best,
Jiang
Hi Jiang, I think there might be something wrong with the definition of your colour palette – have a look at the coolBlueHotRed function I’ve defined and compare the output to the colorRampPalette() function you’re using.
Do you know how can I made a sensitivity analysis in a XYF map developed with R? Is it necessary?
Hi Shane,
I have a 10X10 map with just one empty node. The problem is that this empty node affects the heat map once the function aggregate does not consider this node that is eliminated in the final vector causing an undesirable shift effect in the heat map. Do you know how to avoid it?
Hey John, its a good question, I actually tackled this exact situation recently and had to re-write some of the code to plot this. The key is to find out what nodes are missing from the aggregation, and then to replace these before plotting. This works for me:
var_unscaled <- aggregate(as.numeric(data_train_raw[[variable]]), by=list(som_model$unit.classif), FUN=mean, simplify=TRUE) names(var_unscaled) <- c("Node", "Value") # Add in NA values for non-assigned nodes. # find missing nodes missingNodes <- which(!(seq(1,nrow(som_model$codes)) %in% var_unscaled$Node)) # Add them to the unscaled variable data frame var_unscaled <- rbind(var_unscaled, data.frame(Node=missingNodes, Value=NA)) # order this data frame var_unscaled <- var_unscaled[order(var_unscaled$Node),] plot(som_model, type = "property", property=var_unscaled$Value, main=names(data_train)[var], palette.name=coolBlueHotRed) I'm adding this to the main article also - good question!
Hi Shane,
It works fine for me now. Thank you for your help.
Best regards,
John J
does someone know how to perform a sensitivity analysis on xyf Kohonen map?
Hey Manuel, apologies, I missed your comment previously. Unfortunately this is not something that I have experience in. What are you trying to achieve with the sensitivity analysis?
Hi, well I am try to test the relation between input and output variables in the xyf map. I have a matrix of species by fishery trip and I am looking for the internal structure of the fleet in relation to fish catched by fishermen, despiting that they use the same gear.
Thank you very much Shane for this contribution. It helped me to understand quickly the main concepts behind SOM and how to use it in R.
I want to add that SOM can be used also for prediction and for detecting anomalies. These are the main uses we give to SOM in my work.
Regards
Juan JC
[…] Self-Organising Maps (SOMs) are an unsupervised data visualisation technique that can be used to visualise high-dimensional data sets in lower (typically 2) […]